编码实践当中涉及的密码学知识
OpenSSL
是用于安全传输层(TLS,Transport Layer
Security)协议和安全套接字层(SSL,Secure
Sockets Layer)协议的的工具包,提供了 SSL
协议实现(SSLv2、SSLv3、TLSv1)、大量算法实现(对称/非对称/摘要)、大数运算、非对称算法密钥、ASN.1
编解码库、证书请求(PKCS10)编解码、数字证书编解码、CRL
编解码、OCSP 协议、数字证书验证、PKCS7
标准实现和 PKCS12 个人数字证书格式实现等功能。

然而一直以来 OpenSSL 代码质量,总是受到开发人员的各种诟病,因而出现了 WolfSSL 与 PolorSSL 等 OpenSSL 的开源替代产品,其中 PolarSSL 被 ARM 公司收购之后,现更名为 Mbed TLS,主要由 Trusted Firmware 组织进行维护,遵循相关的 ARM 规范,并为 Armv8-A、Armv9-A、Armv8-M 内核架构提供了安全可信的参考实现。本文主要主要讨论了 Base64 与 Hash 编码、以及 OpenSSL 所涉及的相关加解密知识。
Base64 编码
Base64 是一种基于 64
个可打印字符来表示二进制数据的方法,因为 \(\log_2 64 = 6\),所以每 6 bits
为一个单元,对应某个可打印字符。例如 3 Bytes 相当于
24 bits,对应于 4 个 Base64 单元,即
3 个字节可由 4 个可打印字符来表示。Base64
编码常被用于表示、传输、存储一些二进制数据。
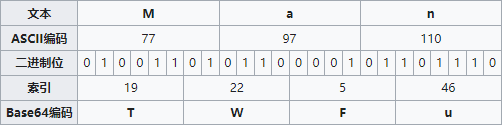
Base64 当中的可打印字符包括字母 A-Z 和
a-z,以及数字 0-9 共有 62
个字符,此外还包括 2
个可打印的符号,在不同的操作系统当中表现不同:
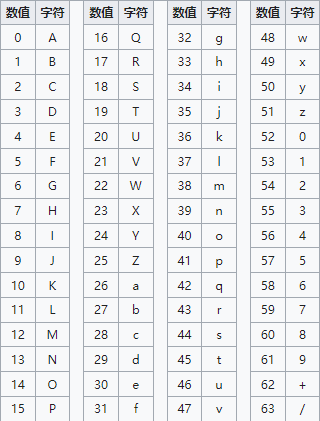
注意 1:标准 Base64 编码并不适用于在 HTTP 环境下通过 URL 传递较长的信息,这是由于 URL 编码器会将标准 Base64 当中的
/和+字符转换为形如%XX的形式,由于标准 SQL 语句当中将%符号用作通配符,而这些%号在存入数据库时还需要再一次进行转换。为了解决这个问题,可以采用一种用于 URL 的改进 Base64 编码,其并不会在末尾填充=号,并将标准 Base64 中的+与/分别修改为-和_,从而免去了在 URL 编解码和数据库存储时所需要进行的额外转换,避免了编码信息长度在此过程中的增加,并且统一了数据库、Web 页面表单的标识符格式。
注意 2:除此之外,还有一种用于正则表达式的改进 Base64 编码变种,其将
+和/分别修改为!和-,这是由于+,*、[、]在正则表达式当中可能具有特殊含义。
Hash 散列函数
散列函数(Hash)又称为散列算法或者哈希函数,可以将任意长度的输入通过散列算法转换为固定长度的散列值输出,Hash 算法没有固定的公式,只要符合散列思想的算法都可以称为 Hash 算法。目前常见的散列算法可以参见下面的表格:
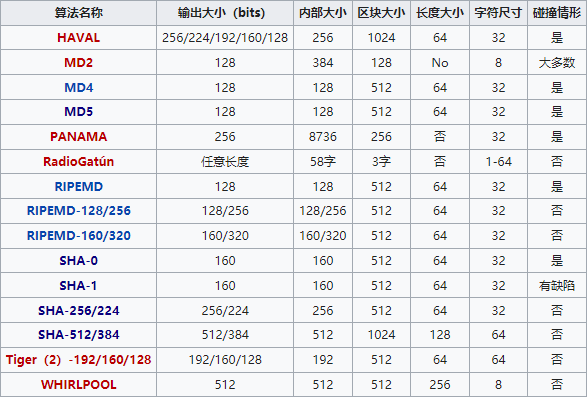
所有的散列函数算法都具备如下 2 个基本特征:
- 如果两个散列值是不相同的,那么这两个散列值的原始输入也是不相同的,具有这种性质的散列函数称为单向散列函数;
- 散列函数的输入与输出不是一一对应关系,如果 2 个输出散列值相同,那么 2 个输入值可能相同也可能不同,这种情况称为散列碰撞;
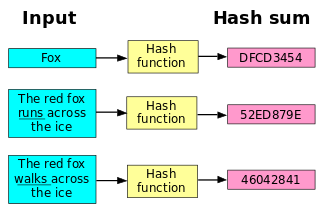
注意:利用散列算法所计算出来散列值的不可逆性(无法逆向演算回原本的数值),可以将其用于加密存储在数据库当中的密码字符串,从而有效的保护密码。
MD5 消息摘要算法
消息摘要算法(MD5,Message-Digest
Algorithm)通过输入不定长度信息,输出四组 32
位数据,最后组合成为一个固定长度的 128 bits/16 Bytes
散列值,通常用于确保数据传输的完整性。该算法是由美国密码学家罗纳德·李维斯特(Ronald
Linn Rivest)设计,于 1992 年公开,但是已于 1996
年在理论上被证实存在破解可能性,并最终于 2004
年被证实无法防止碰撞攻击,因而不再适用于安全性认证。
1 | 输入字符串: |
注意:MD5 加密后的位数有
16 Bytes和32 Bytes两种,其中16 Bytes实际上是取32 Bytes字符串中间的第9 ~ 24位部分。
SHA 安全散列算法
安全散列算法(SHA,Secure Hash Algorithm)包含了一系列密码散列函数算法,可以计算出一个消息所对应的固定长度字符串(称为消息摘要),如果输入的消息不同,那么对应的消息摘要也会不同。SHA 家族算法由美国国家安全局(NSA)设计,并由美国国家标准与技术研究院(NIST)发布:
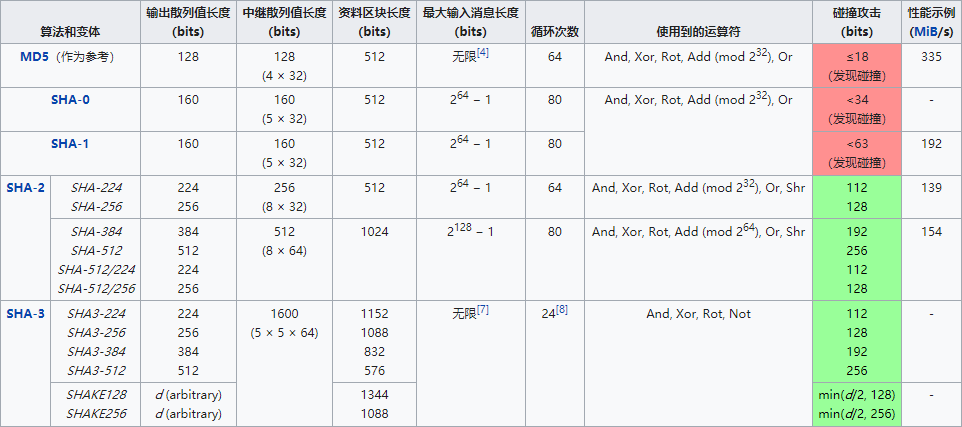
- SHA-0:1993 年发布,当时称做安全散列标准(Secure Hash Standard),发布之后很快就被 NSA 撤回;
- SHA-1:1995 年发布,在许多安全协议中广为使用(包括 TLS 和 SSH),被视为 MD5 的后继者,于 2017 年被荷兰密码学研究小组正式宣布攻破;
- SHA-2:2001 年发布,包括
SHA-224、SHA-256、SHA-384、SHA-512、SHA-512/224、SHA-512/256,虽然至今尚未出现对该版本算法的有效攻击,但是其算法本质上与 SHA-1 基本类似; - SHA-3:2015 年正式发布,由于出现了对于 MD5 的成功破解,以及 SHA-0 和 SHA-1 已经出现理论上的破解方法,于是 NIST 推出了该版本的加密散列算法;
CRC 循环冗余校验
循环冗余校验(CRC,Cyclic Redundancy Check)可以根据文件等数据,利用除法及余数的原理,产生简短的固定位数校验码,也属于一种散列函数算法,主要用于校验数据传输完成之后可能出现的错误,能够高比例的纠正数据传输过程当中的错误,并在极短的时间内完成数据校验计算,该方法由 W.Wesley Peterson 于 1961 年发表。
对称与非对称加密
对称加密算法(Symmetric-key
Algorithm)又称为私钥加密、共享密钥加密,属于密码学当中的一类加密算法。这类算法在加密和解密时使用相同的密钥(或者两个可以简单相互推算的密钥),这组密钥将会多个成员之间的共同秘密,以便维持专属的通信联系。与公开密钥加密相比,要求双方获取相同的密钥是对称密钥加密的主要缺陷之一。常见的对称加密算法有
AES、ChaCha20、3DES、Salsa20、DES、Blowfish、IDEA、RC5、RC6、Camellia
等等。
非对称式加密算法(Asymmetric Cryptography)也称为公钥加密算法(Public-key Cryptography),同样属于密码学当中的一种算法,其加解密过程需要公开密钥(用于加密)和私有密钥(用于解密)2 个密钥,使用公钥将明文加密之后所得到的密文,只能使用对应的私钥才能解密并且得到原来的明文,最初用于加密的公钥并不能用作解密。由于加密与解密需要 2 个不同的密钥,所以被称为非对称加密;
- 加密:将数据转换为不可直接阅读的形式(即密文);
- 解密:将密文转换成能够直接阅读的数据(即明文);
注意:相比较于加密与解密都要使用同一个密钥的对称式加密,非对称式加密的公钥可以任意向外发布,但是私钥必须自行严格秘密保管,绝不能透过任何途径向外提供。此外,对称加密的速度远远快于非对称加密。
DES 数据加密标准
数据加密标准(DES,Data Encryption Standard),是一种在过去主要使用的对称加密算法,1977 年被认定为联邦资料处理标准(FIPS),但是现在已经并非一种安全的加密方法。而 DES 算法的继任者三重数据加密(3DES,Triple DES),本质上相当于是对每个数据块运用 3 次 DES 加密,它并非一种全新的块密码算法,并且在理论上也存在破解方法。
注意:DES 和 3DES 标准目前已经逐渐被高级加密标准(AES)所取代。
AES 高级加密标准
高级加密标准(AES,Advanced Encryption Standard),属于美国联邦政府采用的一种区块加密标准,该标准用于替换原先的 DES,由美国国家标准与技术研究院(NIST)于 2001 年 11 月 26 日发布,并于 2002 年 5 月 26 日成为有效标准,目前已经成为对称密钥加密里最为流行的算法之一。
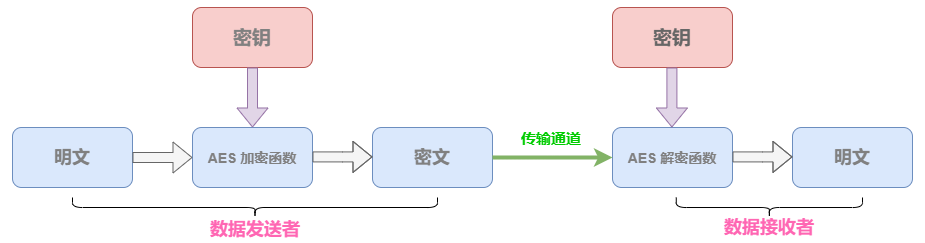
- 明文:没有经过加密的原始数据;
- 密文:已经经过 AES 加密函数处理之后的数据;
- 密钥:用于加密明文的密码,对称加密算法当中用于加解密的密钥相同,密钥由接收者与发送者协商产生(为了防止密钥泄漏,需要避免直接在网络上进行传输,通常经过非对称加密算法加密密钥,然后再透过网络传输给对方);
- AES
加密函数:将明文与密钥作为
AES 加密函数的输入参数,这样 AES
加密函数就会返回密文,即
密文 = AES 加密函数(明文,密钥); - AES
解密函数:将密文与密钥作为
AES 解密函数的输入参数,这样 AES
解密函数就会返回明文,即
明文 = AES 解密函数(密文,密钥);
结构上 AES
将明文划分为一系列长度相等的数据组,每次只加密一组数据,直至加密完整个明文。在
AES 标准规范中,分组长度只能是 128 bits 位,即每个分组为
16 Byte 字节,而密钥的长度可以使用
128 bits、192 bits 或者 256 bits
位,密钥的长度不同,推荐加密轮数也不同,具体请参见下面表格:
| AES | 密钥长度(32 bits) | 分组长度(32 bits) | 加密轮数 |
|---|---|---|---|
| AES-128 | 4 |
4 |
10 |
| AES-192 | 6 |
4 |
12 |
| AES-256 | 8 |
4 |
14 |
RSA 非对称加密算法
RSA 是一种非对称加密算法,由 Ron Rivest、Adi Shamir、Leonard Adleman 三位麻省理工学院的学者于 1977 年共同提出,RSA 就是由 3 位的姓氏首字母组成。对于极大整数做因数分解的难度决定了 RSA 算法的可靠性(假如找到一种快速因数分解的算法,那么 RSA 的可靠性就会极度下降,但找到这样算法的可能性微乎其微),RSA 诞生近半个世纪后的今天,仅有较短的 RSA 密钥才有可能会被暴力破解。除此之外,世界上还没有任何可以攻击 RSA 算法可靠性的方式,只要其密钥的长度足够长,采用 RSA 加密后的信息基本不可能被破解。
下面是一个基于 RSA 算法的典型双向非对称加密握手步骤:
- A 和 B 分别基于 RSA 生成各自的公钥与私钥,然后 A、B 分别将自己的公钥交给 CA 服务器,从而获得公钥证书;
- 当 A 与 B 进行通信时,首先双方会交换公钥证书进行身份认证,然后由 A 生成随机字符串作为对称密钥,并使用 B 的公钥进行加密,然后将其发送给 B;
- B 接收之后使用自己的私钥提取该对称密钥,从而完成双向非对称加密的握手步骤;
使用 OpenSSL 进行签名与验证
签名文件
使用 OpenSSL 签名一个文件需要使用到私钥,可以通过下面的命令创建 OpenSSL 公私钥对:
1 | 生成保存私钥的文件 private.pem |
上述命令中的 <phrase> 密码短语用于加密存储在
private.pem
文件里的私钥,出于安全的原因,建议使用
4096 bits 位的私钥,具体原因可以参见 《RSA
Key Sizes: 2048 or 4096
bits?》一文。当命令执行完毕之后,私钥将会被保存在当前目录下的
private.pem 文件,而公钥则会被保存在
public.pem 文件。
【示例】:将 <phrase>
密码短语设置为 Hank,然后使用 OpenSSL
命令生成私钥文件:
1 | ➜ sudo openssl genrsa -aes128 -passout pass:Hank -out private.pem 4096 |
【示例】:然后,再通过上面得到的
private.pem 文件,来生成对应的公钥文件
public.pem:
1 | ➜ sudo openssl rsa -in private.pem -passin pass:Hank -pubout -out public.pem |
Base64 编码
拥有了公钥与私钥之后,接下来就可以使用
OpenSSL 签名一个文件,这个过程当中将会要求提供密码短语
<phrase>。由于过去 OpenSSL
签名的默认输出格式为二进制,如果希望在互联网上进行传输,则需要采用
Base64 对签名文件进行编码转换:
1 | 基于私钥生成签名文件 |
上述语句中的 <private-key>
是包含私钥的文件,<target-file> 为待签名的文件,而
<base64-signature> 为 Base64
格式的数字签名的文件名,操作完成之后签名文件将会保存为 /opt
目录下的 signature.sha256 文件。
【示例】:使用前一步生成的私钥文件
private.pem 对当前目录下的 uinika.c
文件进行签名,得到一个二进制签名文件 signature.sha256:
1 | ➜ sudo openssl dgst -sha256 -sign private.pem -out signature.sha256 uinika.c |
【示例】:将 /opt 目录下的二进制文件
signature.sha256 转换为 Base64 编码的
signature.base64 文件:
1 | ➜ sudo openssl base64 -in signature.sha256 -out signature.base64 |
注意:目前新版本的 OpenSSL 签名文件,已经可以正常在互联网上传输,不需要再进行额外的 Base64 编码。
验证签名
将签名从 Base64 编码重新转换回二进制文件,并使用前面得到的公钥来验证该签名文件:
1 | 将签名文件从 Base64 编码还原为二进制格式 |
上述命令当中的 <base64-signature> 是包含 Base64
签名的文件,而 <public-key>
是包含公钥的文件,<target-file>
则是待验证的二进制签名文件。验证成功之后,OpenSSL 将会提示
Verified OK,否则就会提示
verification Failure。
【示例】: 把 Base64 编码的签名文件
signature.base64 还原为二进制格式的签名文件
signature.sha256:
1 | ➜ sudo openssl base64 -d -in signature.base64 -out signature.sha256 |
【示例】:通过目标文件 uinika.c
和公钥文件 public.pem 校验还原得到的
signature.sha256 是否有效:
1 | ➜ sudo openssl dgst -sha256 -verify public.pem -signature signature.sha256 uinika.c |
安全套接层 SSL / 传输层安全 TLS
传输层安全性协议(TLS,Transport Layer
Security)以及其前身安全套接层(SSL,Secure
Sockets
Layer)都属于一种安全协议,目的是为互联网通信提供安全以及数据完整性保障。网景公司(Netscape)于
1994 年推出第 1 版网页浏览器时发布了 HTTPS 协议,并以 SSL 进行加密,后来
IETF 将 SSL 进行标准化,于 1999 年公布了
TLS 1.0,随后又于 2006 年公布了 TLS 1.1,2008
年公布了 TLS 1.2,以及在 2018 年公布的
TLS 1.3,目前该协议已经成为互联网加密通信的工业标准。
TLS 协议采用主从式架构模型,用于在网络上的 2
个应用程序之间创建安全的连接,防止在交换资料时受到窃听以及篡改。TLS
协议与高层的 HTTP、FTP、Telnet
等应用层协议并不会产生耦合,这些应用层协议透明的运行在 TLS 之上,由 TLS
进行创建加密通道需要的协商与认证,应用层协议传送的数据通过 TLS
协议时都会被加密,从而保证通信的私密性。
TLS 协议必须在客户端与服务器分别配置之后才能使用,一旦客户端和服务器都同意使用 TLS 协议,那么它们会通过一个握手过程,协商出一个带有状态的连接用于传输数据,如下就是握手建立的具体步骤:
- 客户端连接到支持 TLS 协议的服务器,要求创建安全连接并且列出了受支持的密码包(包括加密和散列算法等);
- 服务器从该列表中确定好密码包,并且通知客户端;
- 服务器返回其数字证书,该证书通常包含有
服务器的名称、受信任的证书颁发机构(CA)、服务器的公钥; - 客户端确认其颁发证书的有效性;
- 为生成用于安全连接的会话密钥,客户端使用服务器的公钥加密随机生成的密钥,并将其发送至服务器,此时只有服务器才能使用自己的私钥进行解密;
- 利用随机数,双方生成用于加密和解密的对称密钥,从而完成 TLS 协议的握手过程;
注意:握手完毕之后的连接是安全的,直到该连接被关闭为止;如果上述任何一个步骤失败,TLS 的握手过程就会失败,并且断开所有连接;
公钥数字签名
公钥数字签名也称为数字签名(Digital Signature),其实质就是逆向使用非对称加密体系,即签名者将信息用私钥加密(非对称加密体系下,私钥通常用于解密),然后将公钥发布出去,验证者使用公钥将加密信息解密并且比对消息(非对称加密体系下,公钥通常用于加密)。
概而言之,非对称加密体系下,通常使用公钥加密,私钥解密。而在数字签名当中,则是使用私钥加密(生成签名),公钥解密(验证签名)。
我们可以直接对数据进行签名(即使用私钥加密,其目的是为了签名,而非保密),验证者用公钥正确解密消息,如果和原始数据保持一致,则签名验证成功。通常情况下,我们只会对数据的 Hash 值进行签名(但是计算数据 Hash 值并非数字签名的必要步骤),因为 Hash 值的长度远远小于原始数据的长度,从而使得签名(非对称加密)的效率大幅度提高。
注意:工程实践当中,通常会组合使用加密与签名技术,例如前面提到的 TLS 协议就同时组合了加密与签名。
CA 数字证书认证
数字证书认证(CA,Certificate Authority)是用于实现多方安全通信所提供电子认证,其本质上是由证书签证机构 CA 签发的对于用户公钥的认证。这里的 CA 即指代负责发放与管理数字证书的权威机构,也指代其所承担的位于非对称加密体系当中的公钥合法性校验任务,主要具有如下的作用与特点:
- 如果用户需要获取 CA 证书,就应当向 CA 机构提出申请,CA 机构判别出申请者的身份之后,就会为其分配一个公钥,并将该公钥与其身份信息绑定为一个整体,并为该整体进行签名,这个签名之后的整体就称为证书,最后会将该证书发还给申请者;
- CA 既是证书的签发机构,也是公钥基础设施的核心。它为每个使用公开密钥的用户发放一个数字证书,用于核验证书当中罗列的用户,是否合法的拥有证书当中列出的公开密钥。与此同时,CA 机构的数字签名使得攻击者不能伪造和篡改证书;
- 如果某个用户想鉴别另一个证书的真伪,就需要使用 CA 的公钥对该证书上的签名进行验证,验证通过之后,该证书才会被认为有效;
数字证书的内容包括有
CA 机构的相关信息、公钥用户信息、公钥、CA 机构的签名与有效期
等,目前数字证书的格式与验证方法普遍遵循 X.509
公钥证书格式标准。
X.509 公钥证书格式标准
X.509 是密码学当中公钥证书的格式标准,应用于 TLS/SSL 在内的众多网络协议当中。X.509 证书当中包含有公钥、身份信息(比如网络主机名,组织或个体名称等)、签名信息(即可以是证书签发机构的 CA 签名,也可以是自签名)。
注意:在 X.509 当中,组织机构通过发起证书签名请求(CSR,Certificate Signing Request)来获得一份签名证书。
X.509 拥有如下几种常用的扩展名:
.pem:隐私增强型电子邮件格式,通常为 Base64 格式;.cer、.crt、.der:通常为 DER 二进制格式;.p7b、.p7c:PKCS#7 格式,不包含数据,只包含证书或者 CRL;.p12:PKCS#12 格式,包含证书的同时可能还包含有私钥;.pfx:PFX,在PKCS#12出现之前使用的格式;
注意:PKCS#7 是签名或者加密数据的格式标准,由于证书是可以进行校验的签名数据,所以采用签名数据(SignedData)结构进行表述;而 PKCS#12 则是由 PFX 格式发展而来,用于交换公有或者私有对象的标准格式。
国密算法
国密算法主要是经由《密码管理局》和《密码行业标准化技术委员会》认定的国产密码算法,当前使用较为广泛的主要是以下 5 种:
- 祖冲之序列密码:中国自主研发的流密码算法,是 运用于移动 4G 网络当中的国际标准密码算法,该算法包括祖冲之算法(ZUC)、加密算法(128-EEA3)、完整性算法(128-EIA3)三个部分;
- SM2 椭圆曲线公钥密码算法:即 ECC
椭圆曲线密码机制,但在签名和密钥交换方面不同于
ECDSA、ECDH等国际标准,该标准包括总则、数字签名算法、密钥交换协议、公钥加密算法四个部分; - SM3
密码杂凑算法:给出了杂凑函数算法(哈希、散列)的计算方法与步骤,适用于商业密码应用当中的
数字签名与验证;该算法对输入长度小于 \(2^{64}\) 次方的数据,经过填充与迭代压缩,生成长度为256 bits位的杂凑值,该算法由填充、迭代过程、消息扩展、压缩函数四部分构成。 - SM4
分组密码算法:常用于无线局域网通信,该算法的分组长度和密钥长度均为
128 bits位,加密算法与密钥扩展算法都采用 32 轮非线性迭代结构,其中加解密算法的结构相同,只是轮密钥的使用顺序相反,解密轮密钥是加密轮密钥的逆序; - SM9 标识密码算法:该算法不需要申请数字证书,适用于互联网安全、物联网安全等,典型的应用是采用手机号码、邮件地址作为公钥,实现数据加密、身份认证、通话加密、通道加密等安全应用,并具有使用方便,易于部署的特点;
注意:密码行业标准化技术委员会(CSTC,Cryptography Standardization Technical Committee)是一家国内从事密码标准化工作的非法人技术组织,归属密码管理局领导和管理,主要从事密码技术、产品、系统和管理等方面的标准化工作。
编码实践当中涉及的密码学知识