《PCB 电流与信号完整性设计》读书笔记

《PCB 电流与信号完整性设计》英文名称是《PCB Currents How They Flow, How They React》，作者是 UltraCAD 公司的创办者 Douglas Brooks，全书着重于物理概念，避免复杂的数学推导，阐述了基本电路的电流源、电流造成的信号完整性问题，以及如何解决串扰和电磁干扰问题。主要内容包括：温度漂移、传输线、反射、耦合电流、功率分配、趋肤效应、介电损耗和通孔等，并且给出了每个常见问题的实用设计方案。

全书分为四个部分，其中第一部分电流的性质介绍了电流的基本定义，第二部分基本电路中电流的流动包括了电阻电路、电抗（电容、电感）电路、以及阻抗相关的内容，第三部分则介绍了电压源与电流源，第四部分电路板上的电流则介绍了 PCB 上引入的各种信号完整性问题。

电子与电荷

原子结构

电流是由电子的流动而产生，1A 电流指的是 1S 时间内通过某个位置 1C 的电荷（即 \(6.25 \times 10^{18}\) 个电子）。物质的原子当中包含有 3 种基本粒子：质子（带 1 个单位正电荷）、中子（不带电荷）、电子（带 1 个单位负电荷），其中质子和中子耦合在原子核，而电子则围绕着原子核做圆周运动。自然界当中的稳定元素都呈现电中性，因而任何元素原子当中的质子与电子数量必然相等。

价带 & 导带

价带（Valence Band）是价电子所占据的能量范围，而导带（Conduction Band）则是自由运动的电子所具有的能量范围；价带当中只拥有一个电子的元素，更容易脱离价带进入导带形成自由电子，从而表现为导体；而价带当中拥有多个电子的元素，由于电子则难以脱离价带，从而表现为绝缘体；

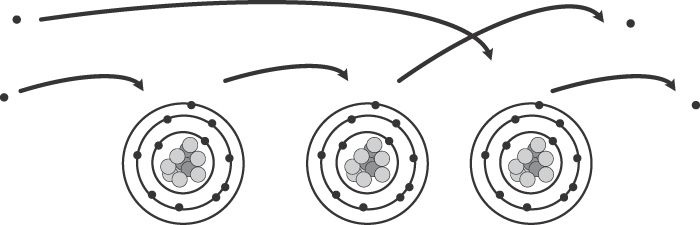
注意：电子带有负电荷，同种电荷相互排斥，异种电荷相互吸引。

电场

可以将带电粒子想象为一个球体，电场将会由该带电粒子向外呈辐射状分布：

磁场

当电子移动产生电流，电流的周边就会产生磁场。这个磁场围绕着电流呈同心圆形式分布，其方向可以通过右手定则来确定：将右手拇指指向电流方向，右手其它手指就会沿着磁场的方向进行弯曲：

注意：电流是单位时间内通过导体某个横截面的电荷量，而电压是电路中自由电荷定向移动形成电流的原因。物理上规定电流的方向是正电荷定向运动的方向，该方向与电子的运动方向相反。

导体的价带上面电子非常松散，绝缘体的价带则几乎被电子填满，而硅、锗等元素的价带正好只被电子填充了一半，二者都有 4 个价电子位于能够容纳 8 个电子的能带之上，这些元素就被称为半导体。

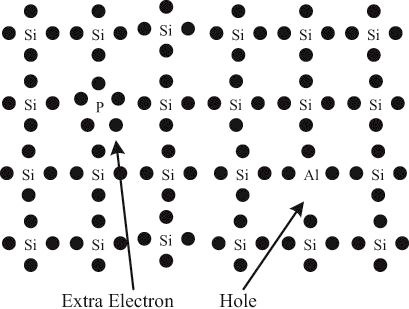
• 将锑、砷、磷等少量价带上只存在 5 个电子的元素添加到硅和锗当中，就会产生多余的电子，称为 N 掺杂（N 表示 Negative 负），进而得到 N 型半导体；
• 将硼、铝、镓等少量价带上只存在 3 个电子的元素添加到硅和锗当中，就会产生大量的空穴，称为 P 掺杂（P 表示 Positive 正），从而得到 P 型半导体；

基本的电流概念

直流 & 交流

直流 DC 是沿着一个方向运动的电流，但是直流并非恒流，其大小可以由电路来决定；而 交流 AC 的方向随着时间呈周期性变化。

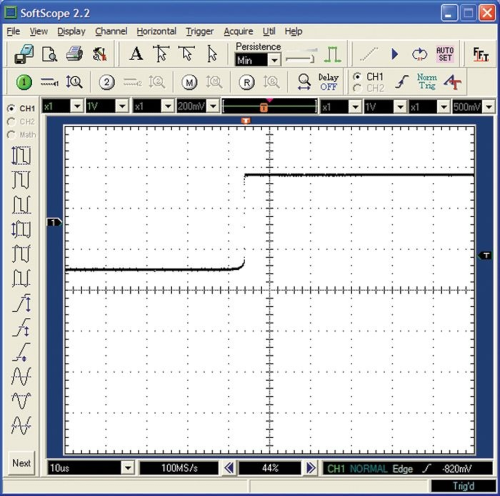
阶跃函数

阶跃函数是一种特殊的连续时间函数，表达的是从 0 到 1 的跳变过程，属于奇异函数。电路分析当中，阶跃函数是研究动态电路阶跃响应的基础。电流或者电压从一个量值变换为另外一个量值的过程，被称作阶跃函数变化，下图展示了一个从低值到高值变化的阶跃函数：

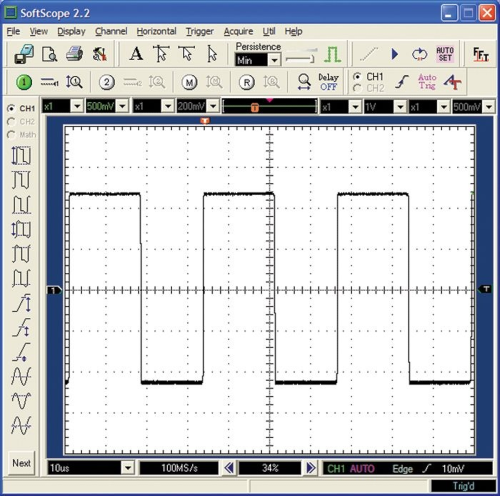
方波

方波是交流电的一种特殊形式，是一种规则的、重复的阶跃变化：

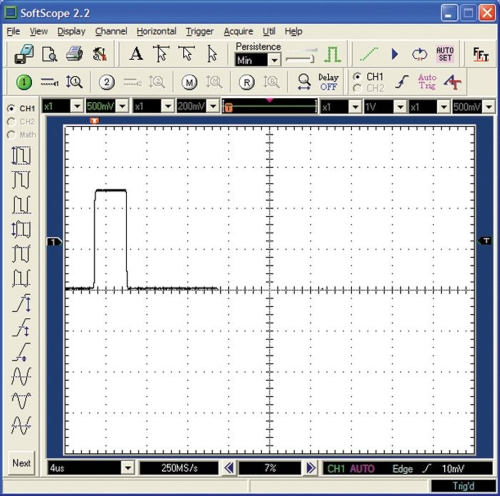
脉冲波

脉冲波看起来像是丢失了部分波形的方波，或者是一种占空比非常低的方波：

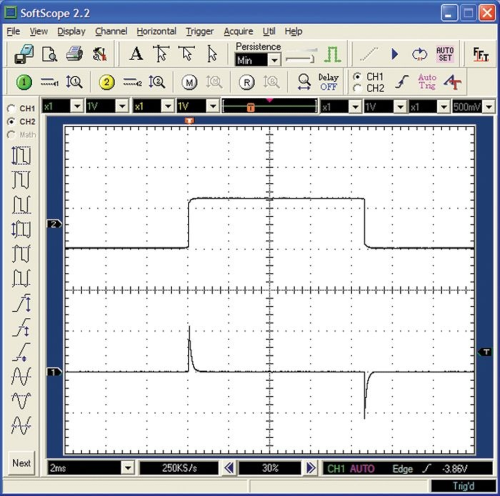
瞬态

瞬态表示的是两种相邻稳定状态之间变化的物理量，例如下图表示的是由电容器上电压的阶跃变化（上方曲线），所引起的流进电容器的瞬态电流（下方曲线）变化：

傅里叶变换

正弦波和余弦波都属于三角函数波形，其它复杂波形到三角函数波形的转换都是通过傅里叶定理完成：任何信号曲线，都可以通过足够数量，具有不同频率（谐波）与相移的三角函数波形叠加而成。

• 谐波是指对周期性非正弦交流量进行傅里叶级数分解，所得到的大于基波频率整数倍的各次分量；
• 基波是指在复杂的周期性振荡当中，与该振荡最长周期相等的正弦波分量；

利用傅里叶变换，可以将一个方波表示为余弦波的无穷级数：

\[ Square(\theta) = \cos(\theta) - \frac{\cos(3 \theta)}{3} + \frac{\cos(5 \theta)}{5} - \frac{\cos(7 \theta)}{7} + ... \]

上述傅里叶级数中的每一项都代表着一个基波频率为 \(\theta\) 的谐波，当使用余弦函数表示方波时，其中只会包含奇次谐波。下图通过多个谐波来表示一个方波，其中的谐波项越多，波形就会越接近方波：

当傅里叶级数的谐波项达到 101 次的时候，波形就已经非常接近于一个标准的方波：

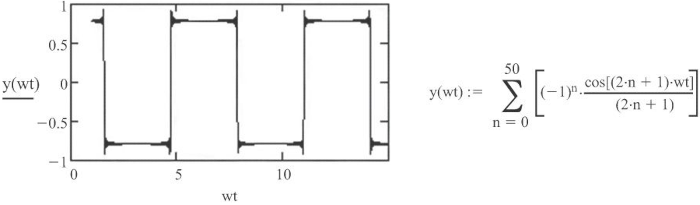
任何波形都可以分解为一系列正弦谐波项，每个谐波项都可以进行单独分析，然后再将结果叠加就可以确定电路的响应。如下分别是锯齿波、三角波、脉冲波三种常见复杂波形的傅里叶级数：

相对介电常数

相对介电常数 \(\epsilon_\tau\) 表达的是材料存储电荷的能力，某种物质当中电磁场的传播速度等于光速除以该物质相对介电常数的平方根：

\[ 信号传播速度 = \frac{11.8}{\sqrt{\epsilon_\tau}} 英寸/纳秒 \]

带状线 & 微带线

设计高速电路板时，通常会存在如下几种常见的走线形式：微带线 a、嵌入式微带线 b、带状线 c、双带状线 d、不对称带状线 e，其中微带线当中信号的传播速度相对要快于带状线。

• 带状线是位于两个参考层之前的走线，无论其位置是居中、双重、偏置还是非对称。
• 微带线则是只在一侧存在参考层的走线，通常其表面为空气或者阻焊油，底面则是电路板材料和参考层；

信号时序

电路能够容忍轻微的信号时序差异，但是如果时序的差异过大，就容易发生采样错误。例如下图中间部分的信号，相对其它信号出现了严重的不一致，导致系统时钟采样信号时发生了跳变：

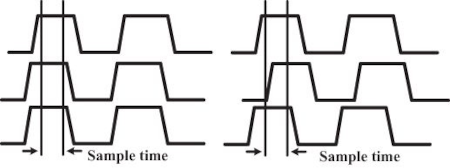
注意：通过设置走线长度可以控制信号的时序，一些 EDA 工具当中可以方便的设置蛇形走线来提供等长的布线。只要蛇形走线具有相应的参考层，并且仅局限于带状线信号层，则不会引发 EMI 电磁干扰问题。

频率

信号的频率可以采用三种方式进行描述：

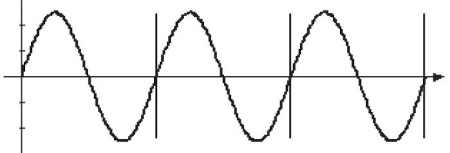
1. 每秒周期数，即 Hz，用符号 \(f\) 表示，上图波形频率为 3Hz，即 \(f=3\)；
2. 每秒波形经过的角度，由于上图正弦波在 1 个周期内经历了 360° 变化，那么 3 个周期内就会经历 \(360° \times 3 = 1080°\)；
3. 角频率，将圆的周长分割为弧度，其中 1 弧度等于圆周上长度等于半径的弧所形成的角度，定义为 1 rad；

圆的周长为 \(2 \pi r\)，其中 \(r\) 为半径，则 360° 圆周的弧度值等于 \(\frac{周长}{半径} = \frac{2 \pi r}{r} = 2 \pi\) 弧度。

因为 \(360°\) 是 \(2 \pi\) 弧度，所以正弦波在 1 秒内可以经过 \(2 \pi f\) 弧度，这就是电子学当中经常使用到的角频率 \(\omega\)，表示的是正弦波在 1 秒钟内经过的弧度数。

\[ \omega = 2 \pi f \]

谐波 & 基波

正弦波通常使用 \(\sin(2\pi ft)\) 或者 \(\sin(\omega t)\) 格式进行表示，这里的 \(2 \pi f\) 或者 \(\omega\) 表示的是 1 秒之内的周期数，\(t\) 表示的是以秒为单位的时间变量。具有 \(\sin(n \omega t)\) 波形的谐波信号，其频率是基波波形 \(\sin(\omega t)\) 的 n 倍，谐波频率与基波频率存在着简单的倍数关系。下图是某个信号的基波及其 4 次谐波：

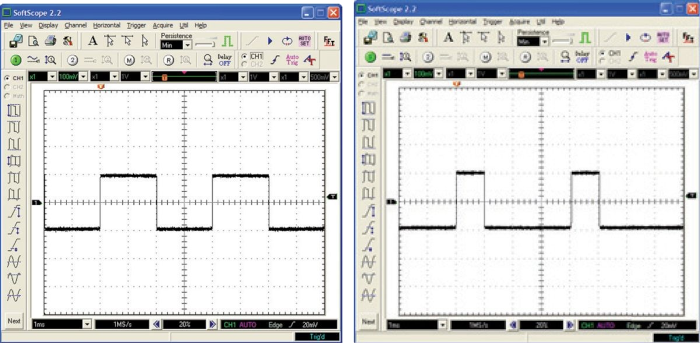
占空比

占空比是指信号处于高电平状态的时间百分比，下图分别表示的是 50%（左）和 25%（右）占空比的方波信号：

频率

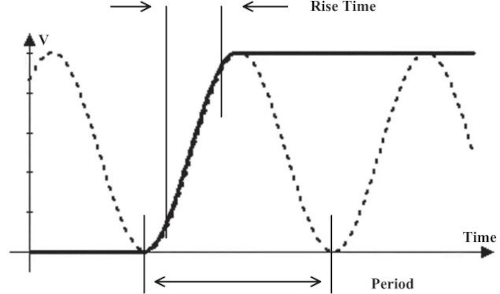
频率是单位时间内电流方向循环改变的次数，但是频率并非高速电路设计当中的主要问题，信号的上升时间才是真正的麻烦所在。下图的正弦波与方波信号具有相同的频率，但是它们的上升时间并不相同：

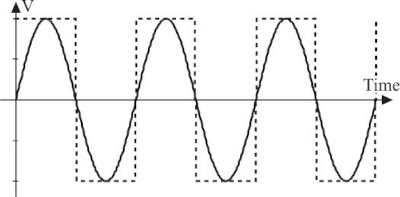
上升时间

信号的上升时间是指从波形 10% 位置上升至 90% 位置所需要的时间长度，而下降时间则是从信号 90% 位置下降至 10% 位置所需的时间长度：

如果电路当中信号变化速度较快，例如电流在 1 纳秒内从 0 mA 变化到 10 mA，则可以将其表示为电流变化量 \(\Delta i\) 除以时间变化量 \(\Delta t\)，当此处的 \(\Delta t\) 小到可以忽略的时候，就可以得到其微分形式 \(\frac{di}{dt}\)，这就是信号完整性问题产生的原因所在。在高速电路当中，\(dt\) 项可以等同于信号的上升或者下降时间。

周期

频率与周期的关系为 \(频率 = \frac{1}{周期}\)，例如具有 1MHz 频率的正弦波周期为百万分之一秒，即 1us 或者 1000ns。

相移

电子学当中的相位通常是指三角函数波形，两个三角函数波形之间的时间差称为相移。如果两个三角函数波形的波峰位于相同的时间点，则认为两者的相位完全相同，称为同相（下图左侧），否则称为不同相（下图右侧）；

• 电阻上的电压与电流完全同相；
• 电容上的电流超前于电压 90°；
• 电感上的电流滞后于电压 90°；

振幅

振幅是指振动的物理量可能达到的最大值，用于表示振动的范围和强度的物理量。

• 峰峰值：一个周期内信号最高值和最低值之间的差值；
• 峰值：是峰峰值振幅的一半，即波形水平中线与其峰值之间的幅度；
• 平均值：对称交流波形振幅总是为零；
• 均方根值：首先将一个波形划分为很多部分，然后求解每个部分振幅的平方，接着计算这些平方值的平均值，最后将平均值开方，就可以得到该波形的均方根值（RMS，Root Mean Square）；

分贝

分贝（dB）是一种基于对数的比率度量单位，其结果与功率密切相关，对应的基本单位是贝尔，两者换算关系如下所示：

\[ 1 贝尔 = 10 分贝 \]

1 贝尔被定义为功率 \(P_1\) 与 \(P_2\) 比值的对数：

\[ 1 贝尔 = log(\frac{P_2}{P_1}) \implies 1 分贝 = \frac{1}{10} 贝尔 = log(\frac{P_2}{P_1}) \cdot \frac{1}{10} \]

时间常数

时间常数表示物理量从最大值衰减到最大值的 \(\frac{1}{e}\) 时所需要的时间，该参数在电子学当中与波形发生改变的时间长度有关，即一个波形变化占据全部波形变化的比例。

白噪声

由于温度引起电子运动而发出的信号，称为热噪声。由于似乎是由所有频率的信号构成，如同白色光线由所有颜色构成一样，所以也被称为白噪声。通常情况下，信号比噪声更大，可以通过信噪比对两者进行比较。

基本定律

回路

电流必须在一个闭合的回路当中进行流动，电流在该回路当中必须处处恒定。

上面电路当中存在 a、b、c 三个回路，基于欧姆定律可以分别得到：

\[ \begin{cases} i_1 = \frac{V}{R_1} = \frac{10}{1000} = 10mA \\ i_2 = \frac{V}{R_2} = \frac{10}{5000} = 2mA \end{cases} \implies i = i_1 + i_2 = 12mA \]

欧姆定律

欧姆定律：电压 V（单位为伏 V）等于电流 I（单位为安 I）乘以电阻 R（单位为欧姆 Ω）：

\[ 电压 V = 电流 I \times 电阻 R \]

注意：欧姆定律作为点概念，适用于电路某个时间的某个特定点。

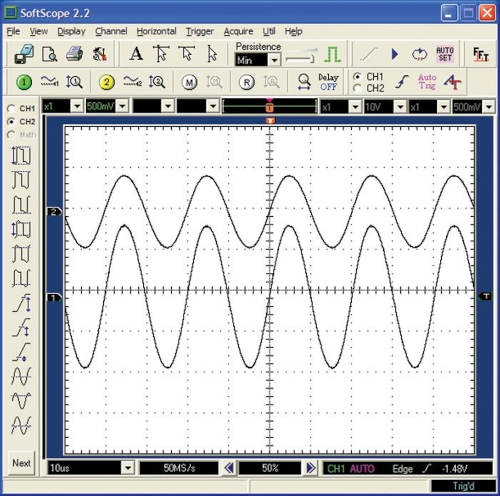
基尔霍夫电流定律

基尔霍夫电流定律：流入某个结点的电流必须等于流出该结点的电流：

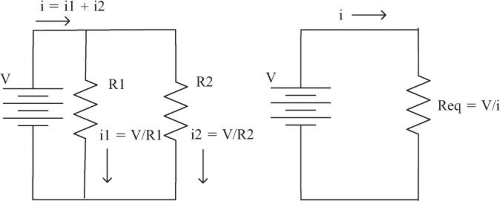
流入上部结点的电流为 \(i\)，流过电阻 \(R_1\) 的电流为 \(i_1\)，流过电阻 \(R_2\) 的电流为 \(i_2\)，根据基尔霍夫电流定律可以得到 \(i = i_1 + i_2\)。根据欧姆定律和基尔霍夫电流定律，可以推导出 n 个电阻并联的等效电阻 \(R_{eq}\) 求解公式：

\[ \begin{cases} i_1 = \frac{V}{R_1} \\ i_2 = \frac{V}{R_2} \\ i = \frac{V}{R_{eq}} \\ \end{cases} \implies \frac{V}{R_{eq}} = \frac{V}{R_1} + \frac{V}{R_2} \implies \frac{1}{R_{eq}} = \frac{1}{R_1} + \frac{1}{R_2} \implies R_{eq} = \frac{1}{\frac{1}{R_1} + \frac{1}{R_2}} = \frac{R_1 R_2}{R_1 + R_2} \implies R_{eq} = \frac{R_1 R_2 ... R_n}{R_1 + R_2 ... R_n} \]

基尔霍夫电压定律

基尔霍夫电压定律：一个回路上的电压之和必然等于零；

将顺时针作为上图电路的参考方向，电阻 \(R_1\) 上的电压降为 \(V_1\)，而电阻 \(R_2\) 上的电压降为 \(V_2\)，电压源上的电压为 \(-V\)，根据基尔霍夫电压定律就可以得到 \(V_1 + V_2 +(-V) = 0\)。结合欧姆定律和基尔霍夫电压定律，同样可以推导出 n 个电阻串联的等效电阻 \(R_{eq}\) 的求解公式：

\[ V_1 + V_2 +(-V) = 0 \implies V = V_1 + V_2 \implies \begin{cases} V_1 = i R_1 \\ V_2 = i R_2 \\ V = R_{eq} \end{cases} \implies iR_{eq} = i R_1 + i R_2 \implies R_{eq} = R_1 + R_2 \implies R_{eq} = R_1 + R_2 ... R_3 \]

电阻电路

电阻率

导体材料对于电流的阻力称为电阻率，例如铜在 20°C 室温下的电阻率为 \(1.724 \mu Ω \cdot cm\)。将电阻率除上材料的横截面积，就可以得到单位长度材料的电阻：

\[ R = \frac{电阻率 \rho}{横截面积 A} \]

PCB 铜泊走线宽度 10mil，厚度 0.65mil，则横截面积 \(10mil \times 0.65mil =6.5 mil^2 = 0.000419354 cm^2\)，将铜的电阻率代入上面公式，就可以得到每厘米走线长度的电阻 \(R\) ：

\[ R = \frac{1.724}{0.000419354} = 4114 \mu Ω/cm \]

1. 电阻反比于横截面积，即横截面积越大，电阻就越小；
2. 电阻正比于长度，走线越长，电阻就越大；
3. 电阻与温度呈函数关系，大多数金属材料的温度越高，电阻就会越大；

注意：焊锡的电阻率是铜的 10~15 倍，因此焊接时需要保持铜质导线之间拥有足够的接触面积。

电阻的电流与相位

电阻与电流、电压的关系遵循着欧姆定律 \(R= \frac{V}{I}\)，除此之外，电阻还会受到信号频率的影响：

• 由于绕线电阻具有线圈，因而具有电容和电感效应，其性能表现为频率的函数；
• 当导体中有交流电或者交变电磁场时，导体内部的电流分布不均匀，电流集中在导体的表面的薄层，越靠近导体表面，电流就会密度越大，导体内部通过的电流较小，致使导体的电阻增加，对应的损耗功率也会增加，这种现象称为趋肤效应（Skin Effect）；
• 普通长度的导线具有寄生电感，因而会在非常快的上升时间内产生频率效应；

电阻的所有频率效应都是由寄生的电感与电容所引起的，并非电阻的性质，电阻本身是独立于频率的，任何在频率范围内绘制成直线的阻抗曲线都表示的是纯电阻：

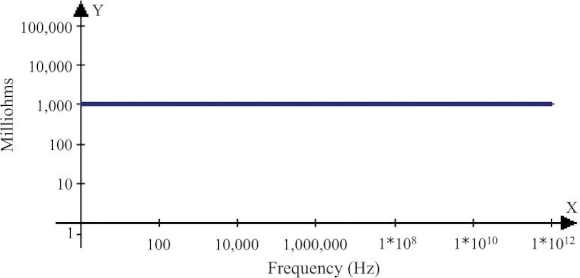
对于交流的电压信号，通过电阻的电流与电压是完全相同的相位，下图是通过电阻的电流信号（上）与电压信号（下）的相位。

串联电阻

电路当中两个电阻 \(R_1\) 和 \(R_2\) 串联的等效电阻 \(R_{eq}\) 等于 \(R_{eq} = R_1 + R_2\)：

并联电阻

电路当中两个电阻 \(R_1\) 和 \(R_2\) 并联的等效电阻 \(R_{eq}\) 等于 \(R_{eq} = \frac{R_1 R_2}{R_1 + R_2}\)：

功率与能量

功率与能量是密切相关的两个概念，其中功率是做功的速率，而能量是功率经过一段时间之后积累的结果。电子学当中的功率可以通过电压乘以电流求解得到：

\[ 功率 P = 电压 V \times 电流 I \]

结合欧姆定律，还可以得到如下的功率计算公式：

\[ \begin{aligned} 功率 P &= \frac{电压 V^2}{电阻 R} \\ 功率 P &= 电流 I^2 \times R \end{aligned} \]

当电流经过电阻时，将会消耗 \(I^2 R\) 的功率，这些消耗的功率会以电阻发热的形式体现，这也正是 PCB 走线容易发热的原因所在。

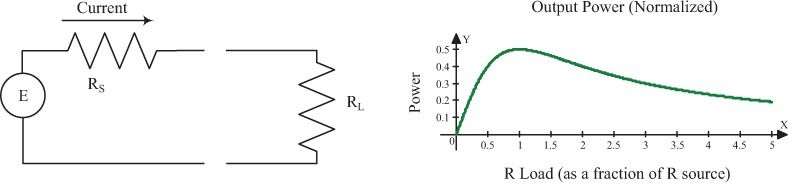
任何电源都可以等效为开路电压 \(E\) 与输出阻抗 \(R_S\) 的串联，而 \(R_L\) 为负载电阻，此时电路所消耗的总功率等于 \(I^2 R_S + I^2 R_L\)。当负载电阻 \(R_L\) 等于输出阻抗 \(R_S\) 时，负载可以从信号源获得最大的输出功率，即阻抗匹配。

电阻分压电路

首先，将两个电阻 \(R_1\) 和 \(R_2\) 串联在一起；然后，将电压 \(E\) 添加在串联电阻的两端，此时两个电阻结合处的输出电压为 \(E_{out}\)，该电路就称为电阻分压电路：

此时，输出电压 \(E_{out}\) 与输入电压 \(E\) 的比值，等于输出端电阻 \(R_2\) 与总电阻 \(R_1 + R_2\) 的比值：

\[ \begin{cases} 回路电流\ i = \frac{E}{R_1 + R_2} \\ 输出电压\ E_{out} = I \times R_2 \end{cases} \implies \frac{E_{out}}{E} = \frac{R_2}{R_1 + R_2} \]

电容

电容的单位是法拉（F），当电容极板上 1库伦 电荷在极板之间产生 1伏特 的电压时，就称该电容为 1F：

\[ 电容\ C = \frac{电荷量\ Q}{电压\ V} \]

电子学术语当中，1F 法拉的电容值比较大，通常采用微法（\(\mu F，10^{-6}F\)）、纳法（\(nF，10^{-9}F\)）、皮法（\(pF，10^{-12}F\)）。电容极板上的电压会伴随充电时间的增加而变大：

\[ \frac{dV}{dt} = \frac{i}{C} \]

直流通过电容器

最初时刻，电子开始流动到电容极板上，由于电容器一个极板的电子会显著多于另一个极板，导致电容极板之间存在着电荷差，进而产生电压；随着时间的推移，电容器极板之间的电压与驱动电压相同，此时将不会再有更多的电子在极板之间流动。

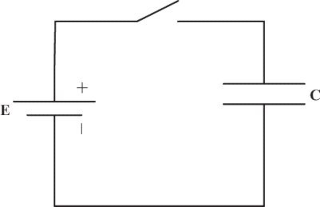
交流通过电容器

由于交流电流的极性反复在发生改变，电容器反复进行充放电，因而电流可以自由的进行流动。

电抗 & 容抗

交流电路当中，阻抗 Z是电阻 R与电抗 X的总和，即 \(Z = R + jX\)，而电抗是阻抗复数公式的虚数部分。电容与电感对于电流所起到的阻碍作用称作电抗，同样采用欧姆作为计量单位，通常使用符号 X 来表示。其中，电容的电抗称为容抗，表示为 \(X_C\)；而电感的电抗称为感抗，表示为 \(X_L\)；

流过电容器的电流大小，取决于电流的频率和电容的大小，并且能够引起电路电流与电压的相位变化。前面已经讨论过，角频率是正弦波在 1 秒钟内所经过的弧度数，即 \(\omega = 2 \pi f\)，由此就可以推导得到容抗的公式：

\[ X_c = -\frac{1}{\omega C} = - \frac{1}{2\pi f C} \]

注意：上面容抗公式中出现的负号，表示通过电容器的电压发生了 -90° 的相移。

欧姆定律同样适用于电抗 \(电压 V = 电流 I \cdot 容抗 X_C\)，其中电压的单位为伏特 V，电流的单位为安培 A，容抗的单位为欧姆 Ω。

容抗与频率的关系

下图为 0.01 uF 电容器的容抗与频率关系曲线，观察可以发现，当频率较高时，电容的容抗比较小；而当频率较低时，电容的容抗比较大；

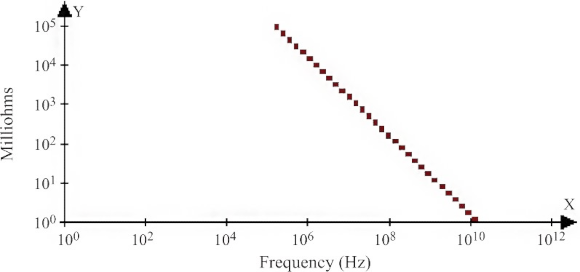
电容的相移

流过的电流曲线为三角波，此时的输出电压曲线为方波：

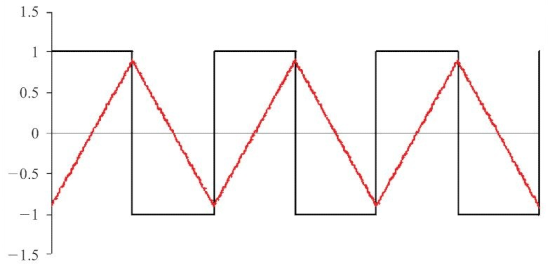
流过电流曲线为正弦波，则此时的输出电压曲线为滞后于电流 90° 的正弦波：

电容的串并联

电容的串并联关系与电阻正好相反，电容 \(C_1\) 和 \(C_2\) 串联之后的等效电容为 \(C = \frac{C_1 \cdot C_2}{C_1 + C_2}\)：

而 \(C_1\) 和 \(C_2\) 电容并联后的等效电容为 \(C = C_1 + C_2\)：

电感

电磁感应现象是指因磁通量变化而产生感应电动势的现象，例如：闭合电路的一部分导体在磁场里做切割磁感线运动时，导体中就会产生感应电流和感应电压。法拉第电磁感应定律是指电路当中感应电压 \(\epsilon\) 与穿过该电路的磁通变化率\(\varPhi\) 呈正比：

\[ 感应电压\ \epsilon = \frac{\Delta \varPhi}{\Delta t} \]

电感的单位是亨利 H，常用的单位有毫亨 mH、微亨 uH、纳亨 nH。当流过 1H 亨利电感器的电流，以 1A 安培每秒的速度进行变化时，就会产生 1V 伏特的电压：

\[ 电感\ L = \frac{电压\ V}{电流变化量\ di / 时间变化量\ dt} \]

直流通过电感器

直流信号通过电感器时，不会产生反向的感生电流，所以理想电感器对于直流不会产生阻抗：

交流通过电感器

交流信号通过电感器时，变化的磁场会产生出反向的感生电流，会阻止电感器的导通：

注意：信号频率越高，电感器对于交流信号的阻抗就越大。

感抗

当线圈中有电流通过时，就会在线圈中形成感应电磁场，而感应电磁场导致线圈当中产生感应电流，从而抵制通过线圈的电流，这种电流与线圈之间的相互作用称为感抗，采用符号 \(X_L\) 进行表示。感抗的大小取决于电感量的大小以及通过信号的频率：

\[ X_L = \omega L \xrightarrow{\omega = 2 \pi f} X_L = 2 \pi f L \]

欧姆定律同样适用于电感，通过电感的电压 \(V\)（伏特 V）等于电流 \(I\)（安培 A）乘以感抗 \(X_L\)（欧姆 Ω）：

\[ V = I \cdot X_L \]

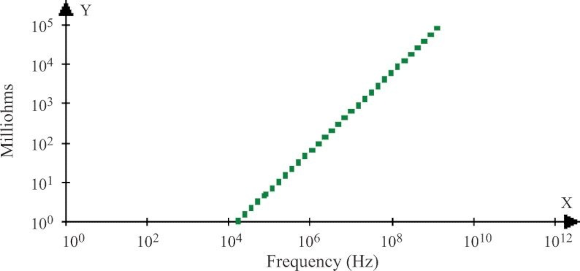
感抗与频率的关系

当频率较低时，感抗较小；而当频率较高时，则感抗将会增大，即感抗伴随着频率的升高而增大：

电感相移

当经过电感的电流为三角波，则电感两端的电压呈现为方波：

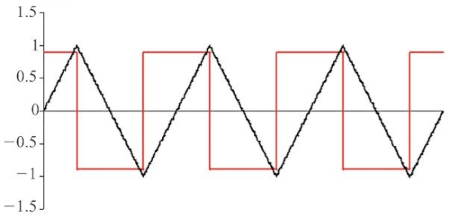
当流经电感的电流为正弦波，则电感两端的电压曲线为超前于电流曲线 90° 的正弦波：

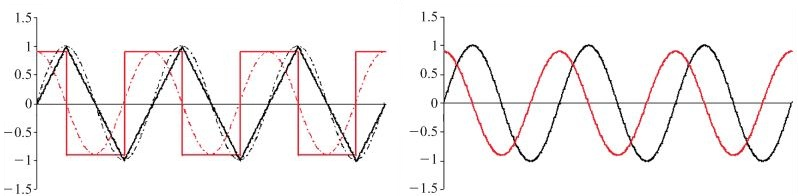
电感的串并联

电感的串并联关系与电阻完全相同，电感 \(L_1\) 和 \(L_2\) 串联之后的等效电感为 \(L_{eq} = L_1 + L_2\)：

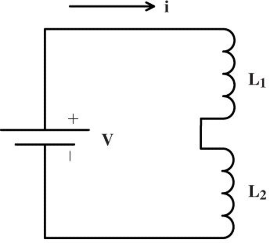
而 \(L_1\) 与 \(L_2\) 并联之后的等效电感为 \(L_{eq} = \frac{L_1 \cdot L_2}{L_1 + L_2}\)：

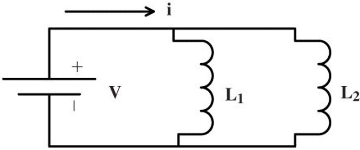
趋肤效应

恒定的电流会在导体截面均匀分布，而交变电流会让导体出现自感电动势，从而抵抗电流的通过，该电动势的大小正比于导体单位时间所切割的磁通量。

以圆形截面的导体为例，越靠近导体的中心位置，所受到自感电动势的影响就越大；而越靠近导线表面的位置，所受到自感电动势的影响就越小，进而导致趋近导体表面处的电流密度较大（上图阴影的深浅就就体现了电流密度）。

注意：由于自感电动势会随着频率的提高而增加，所以趋肤效应也会随频率的提高而增强，造成导体当中通过电流的有效截面积减小，电阻增大。

谐振

对于包含电容、电感、电阻元件的无源一端口网络，其端口可能会呈现出容性、感性、阻性，当电路端口的电压 \(U\) 和电流 \(I\) 出现相同的相位，电路呈现阻性时，就称为谐振现象，这样的电路就称为谐振电路。

串联谐振

对于一个由电感 \(L\) 与电容 \(C\) 串联起来组成的电路：

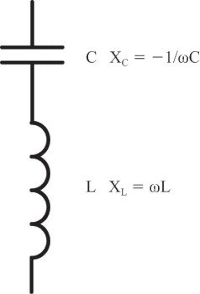
这个电路的总电抗可以通过 \(X_{总} = X_C + X_L\) 计算得到：

\[ X_{总} = X_C + X_L \implies \begin{cases} X_C = - \frac{1}{\omega C} = -\frac{1}{2 \pi f C} \\ X_L = \omega L = 2 \pi f L \end{cases} \implies X_{总} = X_C + X_L = -\frac{1}{\omega C} + \omega L \]

此时如果 \(\frac{1}{\omega C} = \omega L\)，就可以推导得到：

\[ \omega = \frac{1}{\sqrt{LC}} = 2 \pi f \]

当电容值为 0.01uF，而电感值为 10nH 时，代入上面方程可以求解得到频率 \(f\) 的值为 16MHz，即通过频率为 16MHz 的信号时，这个 LC 串联电路的阻抗等于零：

\[ f = \frac{1}{2 \pi \sqrt{LC}} = \frac{1}{2\pi \sqrt{0.01\times10^{-6} \times 10 \times^{-9}}} = 16MHz \]

下图左右两侧曲线，分别为感抗和容抗曲线，两者相交于 16MHz 位置，由于两者的符号相反，所以正好完全抵消，电抗急剧下降到零：

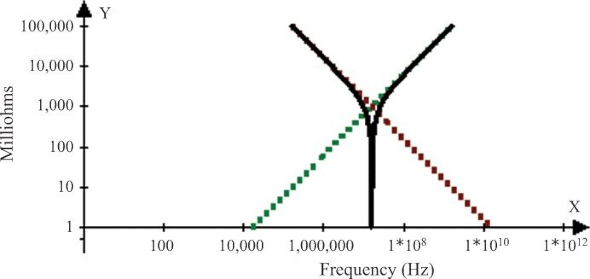
由电感和电容组成的串联电路，当容抗 \(X_C\) 与感抗 \(X_L\) 相等时，电路当中电压与电流的相位相同，电路总体呈现阻性，这种现象就称为串联谐振。此时，电路的总阻抗最小，电流将会达到最大值，电感和电容上会产生高于电源许多倍的电压，因而也被称为电压谐振。此时，容抗 \(X_C\) 与感抗 \(X_L\) 相等时的频率点，就称为谐振点。

并联谐振

相应的，电感与电容并联之后的电抗与电阻的并联相类似：

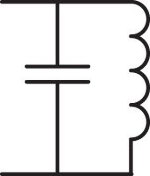
此时该电路的总电抗 \(X_{总}\) 可以通过下面的过程推导得到：

\[ X_{总} = \frac{1}{\frac{1}{X_L} + \frac{1}{X_C}} = \frac{1}{\frac{L}{\omega L} - \omega C} = \frac{\omega L}{1 - \omega^2 LC} \]

此时，当并联的电容值为 0.01uF，而电感值为 10nH 时，谐振点依然为 16MHz，但是在此时电抗将会趋于无穷大：

由电感与电容组成的并联电路当中，当电容的容值使得电路上的电压与电流处于相同的相位，电源提供的电能全部被电阻所消耗，成为电阻电路时，就被称为并联谐振。此时电路的总阻抗最大，而总电流最小，但是支路的电流可能大于总电流，因而并联谐振也被称作电流谐振。

阻抗

阻抗的定义

阻抗是电阻和电抗共同作用的结果，通常使用字母 Z 来进行表示，其复数表达式为：

\[ Z = R + jX \]

上面方程当中的 \(R\) 表示电阻分量，\(X\) 表示电抗分量，而 \(j\) 的值为 \(\sqrt{-1}\) 称为虚数单位。

阻抗的大小

阻抗是通过从原点指向电阻 \(R\) 与电抗 \(X\) 交点的向量来进行表示的。

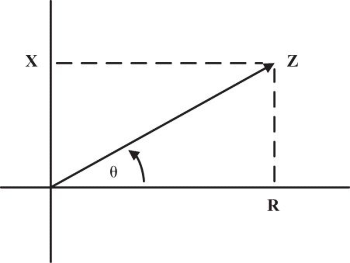
上图坐标轴当中的原点、\(X\) 轴、\(R\) 轴构成了一个直角三角形，根据三角函数的关系可以得到：

\[ Z = \sqrt{R^2 + X^2} \]

例如在下面电路当中，\(100Ω\) 电阻与 \(0.02 \mu F\) 电容串联在一起：

如果此时频率 \(\omega = 10^6\)，从而可以得到如下推导过程：

\[ \begin{cases} R = 100Ω \\ X_C = -\frac{1}{\omega \times 0.02 \times 10^{-6}} \end{cases} \implies \begin{cases} R = 100Ω \\ X_C = -\frac{1}{10^6 \times 0.02 \times 10^{-6}} \end{cases} \implies \begin{cases} R = 100Ω \\ X_C = -50Ω \end{cases} \]

根据上面的推导结果，就可以将上面电路的阻抗关系绘制到如下坐标轴上：

根据上述阻抗向量公式，可以得到该电路的阻抗为 \(Z = \sqrt{100^2 + (-50)^2} = 111.8\)。此时，如果将频率改变为 \(\omega = 10^7\)，则会使得容抗 \(X_C = -\frac{1}{10^7 \times 0.02 \times 10^{-6}} = -5Ω\)，此时该电路的阻抗应为：

\[ \begin{cases} R = 100Ω \\ X_C = -5Ω \end{cases} \implies Z = \sqrt{100^2 + (-5)^2} = 100.1 \]

由此，就可以得到频率为 \(\omega = 10^7\) 时，串联 \(100Ω\) 电阻与 \(0.02 \mu F\) 电容的阻抗图：

可以看到，高频状态下的容抗值会比较小，决定阻抗值大小的主要是串联的电阻。

阻抗的相位角

阻抗的相位角就是下图当中的 \(\theta\) 角，是阻抗向量与 \(R\) 横轴之间的夹角。如果这个角为负（阻抗向量指向下方），那么该电路是容性。如果这个角为正（阻抗向量指向上方），那么该电路为感性。

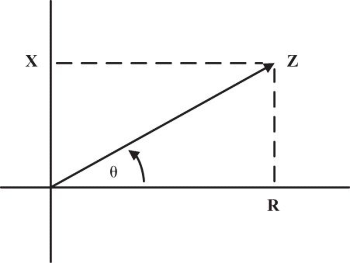
阻抗的相位角存在着 3 种特殊情形：

1. 相位角为 +90°：阻抗向量与 X 轴正半轴重合，电路表现为纯感性；
2. 相位角为 -90°：阻抗向量与 X 轴正半轴重合，电路表现为纯容性；
3. 相位角为 0°：阻抗向量与 R 轴重合，电路表现为纯阻性；

结合三角函数的知识，角 \(\theta\) 的正切是对边与邻边的比值，由此可以知道角 \(\theta\) 等于对边与邻边比值的反正切：

\[ \tan(\theta) = \frac{X}{R} \implies \theta = \tan^{-1}(\frac{X}{R}) \]

对于前述的示例电路，可以计算得到如下结果：

\[ \begin{cases} 当 \omega = 10^6 时：\tan^{-1}(\frac{-50}{100}) = \tan^{-1}(-0.5) = -26.6° \\ 当 \omega = 10^7 时：\tan^{-1}(\frac{-5}{100}) = \tan^{-1}(-0.05) = -2.9° \end{cases} \]

阻抗的相位角代表了该电路电压与电流之间的相位差，相位角为负则表示当前电路的电压滞后于电流的相位，当频率增加之后，由于高频信号的电容效应会下降，电压相位的滞后程度也会减少。

下图是频率为 \(\omega = 10^6\) 时，电路当中各处电压的波形：

下图是频率为 \(\omega = 10^7\) 时，电路当中各处电压的波形：

分析上述两组图形，可以得出如下三点结论：

1. 通过电阻器的电流 \(I_R\) 与电压 \(V_R\) 同相，并且电容器上的电压 \(V_C\) 滞后于电阻器上的电压 \(V_R\) 与电流 \(I_R\) 有 90° 度；
2. 尽管电容器上的电压 \(V_C\) 伴随频率的提高而变小，但是总电压 \(V_{Total}\) 并未发生变化；
3. 当频率为 \(\omega = 10^6\) 时，总电压 \(V_{Total}\) 滞后于电流（该电流与电阻上的电压 \(V_R\) 同相）26.6° 度；而当频率等于 \(\omega = 10^7\) 时，总电压 \(V_{Total}\) 仅滞后于电流 2.9° 度；

串联 RLC 电路示例

对于下面这个仅由电阻、电感、电容组成的简单 RLC 电路：

列写感抗 \(X_L\)、容抗 \(X_C\)、总阻抗 \(X_{总}\) 的方程，联立之后可以得到：

\[ \begin{cases} X_L = j \omega L \\ X_C = \frac{1}{j \omega L} \\ X_{总} = j \omega L + \frac{1}{j \omega L} \end{cases} \implies \begin{cases} X_L = j \omega L \\ X_C = -\frac{j}{j \omega C} \\ X_{总} = j(\omega L - \frac{1}{\omega C}) \end{cases} \implies Z = R + j(\omega L - \frac{1}{\omega C}) \]

假设电阻 \(R = 10 Ω\)、电感 \(L = 10 nH\)、电容 \(C = 0.01 \mu F\)、频率 \(\omega = 10^7\)，根据上述的推导结果可以得到：

\[ \begin{cases} R = 10 Ω \\ L = 10 nH \\ C = 0.01 \mu F \\ \omega = 10^7 \end{cases} \implies Z = 10 - j9.9 \]

根据前面得到的阻抗 \(Z = \sqrt{R^2 + X^2}\) 与阻抗角 \(\theta = tan^{-1}(\frac{X}{R})\) 公式，还可以推导得到：

\[ \begin{cases} Z = 14.0716Ω \\ \theta = -44.712° \end{cases} \]

如果此时将频率提高至 \(\omega = 10^8\)，就会推导得到：

\[ \begin{cases} Z = 10Ω \\ \theta = 0° \end{cases} \]

已知频率 \(\omega = 2 \pi f\)，由于此时 \(\omega = 10^8\)，所以频率 \(f = \frac{10^8}{2 \pi} = 16MHz\)，这与之前讨论过的 LC 电路的谐振频率相同，从而可以得到如下结论：

1. 在谐振频率处，通过电路的阻抗是纯阻性的；
2. 在谐振频率处，阻抗表达式当中的电抗项等于零；
3. 在谐振频率处，通过电路的相移为 0°；

下图左侧是上述串联 RLC 电路的阻抗与频率的关系，而右侧体现的则是相移与频率的关系：

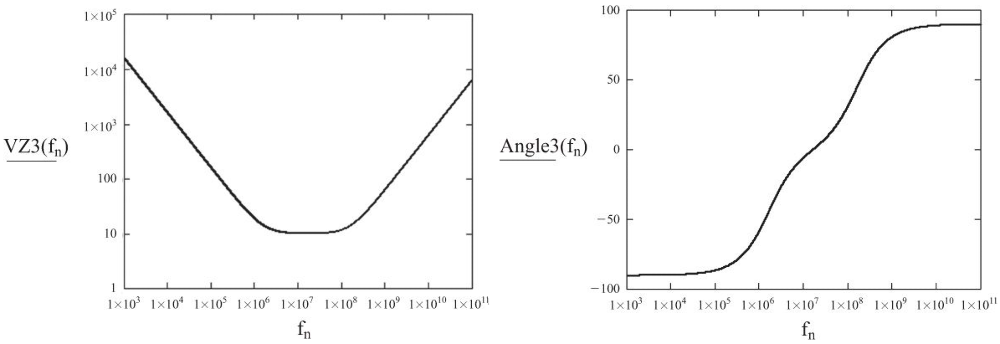
分析上述图像还可以得到如下两个结论：

• 阻抗总是为正，并且谐振频率位置的阻抗最小，相移为零；
• 如果当前频率低于谐振频率（电路呈容性），相移为负；如果高于谐振频率（电路呈感性），则相移为正；其取值范围位于 \(-90°~+90°\) 之间；

分析电阻与电抗电路当中的电压电流，需要处理一些涉及到相移的微妙问题。当频率 \(\omega = 10^7\) 时，阻抗 \(Z = 14.0716Ω\)，阻抗的相位角 \(\theta = -44.712°\)。这里从相移为 0° 的正弦波电压开始分析，先使得最大电压等于 10V，这样就可以得到此时的总电压 \(V_总 = 10 \sin(\theta)\)，再结合欧姆定律就可以得到：

\[ I = \frac{V}{Z} = 0.71065 \sin(\theta + 44.712) \]

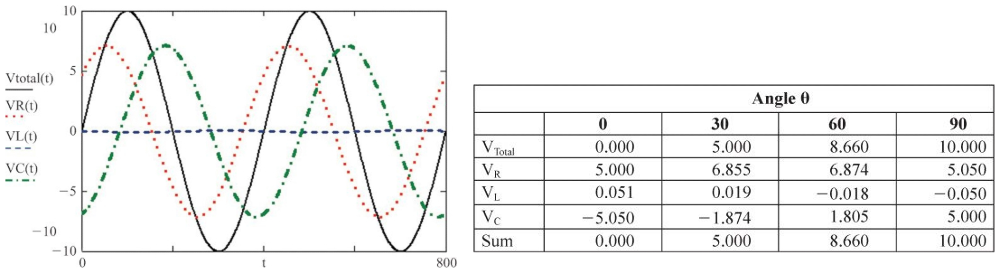
由于该电路为容性，电流超前于电压，电压的相移为负，所以 \(\theta\) 的正弦函数为正。该电路上电感、电阻、电容三个元件上的电压分别等于电流乘以它们各自的电阻或者电抗：

\[ \begin{cases} V_R = I \times R = 7.1061 \sin(\theta + 44.712) \\ V_L = I \times X_L = 0.07106 \{sin(\theta + 134.712)\} \\ V_C = \frac{I}{X_C} = 7.1061 \{sin(\theta - 45.288)\} \end{cases} \]

下图绘制了包括上述 \(V_总\)、\(V_R\)、\(V_L\)、\(V_C\) 四个波形在两个周期内的时序关系，注意它们之间的相位关系：